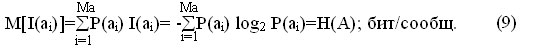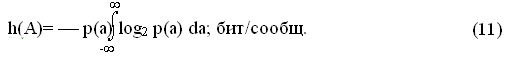Информационные характеристики источников сообщений

Количественная мера информации

Поскольку любая система связи предназначена для передачи информации, то возникает задача в оценке количества информации в передаваемом сообщении. Оценить количество информации с точки зрения ее ценности для получателя невозможно, т. к. одно и тоже сообщения для различных получателей несет различную ценность, так, например, информация получаемая при изучении данного материала для специалиста имеет весьма большую ценность.

Поэтому для определения количества информации используют вероятностные характеристики сообщения, которые не связаны с конкретным содержанием сообщения, а отражают степень их неопределенности (неожиданности). Поскольку информация это новые сведения, то и сообщения менее вероятные несут больше информации, нежели сообщения более вероятные. Таким образом, имеет место обратно пропорциональная зависимость между количеством информации в сообщении и вероятностью его появления.

Также для определения количества информации используются две зависимости:

• линейная выражающая зависимость количества информации в сообщении от его длины,   т. е. например, книга несет больше информации, чем одна ее страница;
• экспоненциальная выражающая зависимость количества информации в сообщении от возможных перестановок одних и тех же элементов этого сообщения, так, например, если источник сообщения имеет словарный запас в 1000 слов и формирует сообщение длинной 50 слов, то количество возможных сообщений будет равно 50¹⁰⁰⁰.

Чтобы учесть обе этих зависимости принимается логарифмическая шкала  для оценки количества информации. Исходя из выше сказанного количество информации в сообщении будет определятся:

I(a_i) = log_b 1/P(a_i) = -log_b P(a_i);

где I(a_i) — количество информации в сообщении a_i;

P(a_i) — вероятность появления сообщения a_i.

Выбор основания логарифма определяет единицу измерения количества информации. Для удобства в качестве основания в системах с двоичными кодами используется основание b=2 и тогда информация измеряется в битах — бинарных или двоичных единицах (от английских слов binary digit). Таким образом, количество информации определяется как:

I(a_i) = -log₂ P(a_i); бит                                                                 (8)

Из данного выражения следует, что один бит информации это:

P(a_i) = 0,5I(a_i)= -log₂ 0,5=1 бит.

т. е. 1 бит ? это количество информации, которое несет сообщение с вероятностью P(a_i)=0,5.

Термин бит используется в вычислительной и импульсной технике, поскольку там используются сообщения формируемые двумя равновероятными символами 1 и 0.

Как следует из выражения, количество информации не может быть отрицательным.

 Энтропия источника

Большинство реальных источников формирует сообщения с различным количеством информации, однако, при решении практических задач необходимо знать среднее количество информации приходящееся на одно сообщение. Среднее количество информации определяется как математическое ожидание количества информации в сообщении.

где Ма — количество возможных сообщений источника.

Величина Н(А) называется энтропией источника и характеризует среднее количество информации приходящейся на одно сообщение.

Приведенное выражение используется для определения энтропии источников дискретных сообщений. Для непрерывных сообщений а(t) энтропия теоретически стремится к бесконечности, т. к. сообщение может принимать бесконечное число значений, следовательно P(a_i)®0, а  I(a_i)®?. Однако если сообщение подвергнуть дискретизации и представить его конечным числом квантованных значений по уровню L, то можно определить среднее количество информации в одном отсчете (энтропию отсчета):

где p_i — вероятность появления в квантованном сообщении i-го уровня.

Lкв — количество уровней квантования.

Если осуществить предельный переход устремив L к бесконечности, то получится величина, называемая дифференциальной энтропией.

Энтропия является объективной информационной характеристикой источника сообщений. Она всегда положительна.

Свойства энтропии.

1⁰ Энтропия равна нулю, если одно сообщение достоверно (P(a_i)=1), а другие не возможны.

2⁰ Энтропия максимальна, когда все сообщения равновероятны, и растет с увеличением равновероятных сообщений.

3⁰ Энтропия обладает свойством аддитивности, т. е. энтропии различных источников можно складывать.

 Избыточность источника

Под избыточностью понимают наличие в сообщении «лишних» элементов, т. е. элементов не несущих смысловой нагрузки (например, союзы, предлоги). Данные элементы могут быть восстановлены за счет статистических взаимосвязей между другими элементами сообщения. Например, союзы, предлоги и знаки препинания можно восстановить, зная правила построения предложений. Таким образом:

избыточность — это мера сокращения сообщения без потери информации, за счет статистических взаимосвязей между элементами сообщения.

Количественной мерой информации является коэффициент избыточности:

c_и= [Hmax(A) ? H(A)]/Hmax(A)                                               (12)

где Н(А) — энтропия, вычисленная на основе учета статистических характеристик сообщений;

Hmax(A) — максимальная энтропия источника, которая согласно второму свойству равна:

Hmax(A)= log₂ Ma; бит/сообщ.                                                 (13)

Наличие избыточности при передаче сообщений имеет свои положительные и отрицательные стороны. Сообщение, обладающее избыточности требует большего времени передачи и, соответственно большего времени занятия канала. Однако повышение избыточности приводит к увеличению помехоустойчивости сообщения. Она способствует обнаружению и исправлению ошибок в принятых сообщениях. Это связано с тем, что для формирования сообщения используются не все возможные комбинации символов, а лишь определенные (разрешенные), которые заносятся в специальные справочники (словари). При приеме сообщения с элементами (словами) которых нет в справочниках говорит о наличии ошибки и ошибочный элемент может быть заменен похожим по написанию или подходящим по смыслу. Все языки обладают избыточностью равной c_и»0,5.

 Производительность источника

Производительность источника — это среднее количество информации создаваемое источником в единицу времени.

Производительность источника дискретных сообщений определяется как:

H’д.с.(А)=Н(А)/tср; бит/с                                                          (14)

где tср — средняя длительность сообщения:

tср=tн/n; с                                                                                   (15)

где tн — время, в течении которого было сформировано n сообщений.

Производительность источника непрерывных сообщений определяется как:

H’н.с.(А)=fд Hотсч(А); бит/с                                                    (16)

где fд — частота дискретизации (2Fmax).

Если сообщение квантуется равновероятными уровнями, т. е. p_i=1/L, то производительность источника может быть определена как:

H’н.с.(А)=fд log₂ L; бит/с                                                          (17)