Скорость передачи информации по каналу — это среднее количество информации, получаемое на выходе канала в единицу времени.
В идеальном канале, т. е. канале без помех количество принимаемой информации соответствует переданной, а соответственно скорость передачи информации равна производительности источника.
В реальном канале, ввиду воздействия помех, происходит потеря части или всей информации. Об этом говорит тот факт, что при разговоре по телефону, из-за шумов, либо других каких либо помех, абонент просит повторить сказанное, так как он не все понял. Поэтому при вычислении скорости передачи информации учитывают эти потери информации величиной, называемой энтропией потерь.
Скорость передачи информации для дискретного канала определяется как:
Rд.к.=[H(U) — Hпот(U)]/tUср; бит/с (18)
где H(U) — энтропия передаваемого дискретного первичного сигнала;
Hпот(U) — энтропия потерь в канале для дискретного первичного сигнала;
tUср — средняя длительность дискретного первичного сигнала.
Скорость передачи информации для непрерывного канала определяется:
Rн.к.=2Fmax[h(U) — hпот(U)]; бит/с (19)
где h(U) — энтропия передаваемого непрерывного первичного сигнала;
hпот(U) — энтропия потерь в канале для непрерывного первичного сигнала;
Fmax — максимальная частота передаваемого первичного сигнала.
Пропускная способность канала — это наибольшее значение скорости передачи информации по каналу электросвязи при заданных ограничениях.
C=maxR. (20)
Под заданными ограничениями подразумевают тип канала (дискретный или непрерывный) и характеристики сигналов и помех.
Пропускная способность дискретного канала определяется по выражению:
Cд.к=.(1/tи) [log2 m+p log2 p/(m — 1)+(1 — p) log2 (1 — p)]; бит/с (21)
где m — количество возможных значений дискретного сигнала;
tи — минимальная длительность дискретного сигнала;
р — вероятность ошибки сигналов в канале.
Величина 1/tи называется скоростью модуляции она показывает количество передаваемых импульсов в секунду. Скорость модуляции обозначается латинской буквой В, единицей измерения является бод.
Из данного выражения следуют частные случаи:
В дискретном идеальном канале (без помех)
Сд.к.=B log2 m; бит/с. (22)
В двоичном канале (m=2)
Сд.к.=B[1+p log2 p + (1 — p) log2 (1 — p)]; бит/с (23)
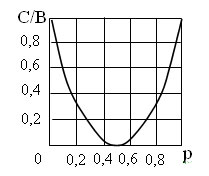
Для двоичного канала зависимость С/В от вероятности ошибки р рассчитанная по данному выражению показана на рисунке 5.
Как видно из рисунка пропускная способность двоичного канала при р=0,5 равна нулю. Этот случай называется обрывом канала. Физически это означает, что вероятность ошибки р=0,5 можно получить и ничего не передавая по каналу. Однако при р=1 пропускная способность канала максимальна и равна пропускной способности идеального канала. Это объясняется тем, что при р=1 производится безошибочный прием сигналов в «негативе», т. е. достаточно инвертировать 0 на 1, а 1 на 0 чтобы восстановить переданный сигнал.
Пропускная способность непрерывного канала определяется по формуле Шеннона:
Сн.к.=?Fк log2 (1+Pc/Pп); бит/с (24)
где ?Fк — полоса пропускания канала;
Рс ? средняя мощность сигнала;
Рп — средняя мощность помехи.
Между производительностью источника и пропускной способностью канала существует взаимосвязь, которая определяется условием согласования источника сообщения с каналом связи:
Для без искаженной передачи сообщения необходимо чтобы производительность источника не превышала пропускную способность канала.
Ни’(А) ? Ск. (25)