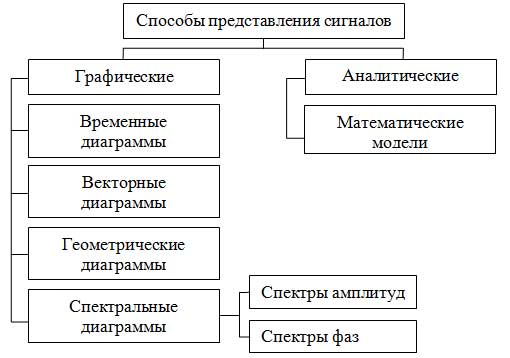
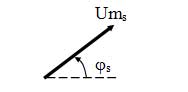Способы представления сигналов электросвязи представлены рисунком 8.
Рисунок 8 - Способы представления сигналов
Временная диаграмма представляет собой график зависимости какого либо параметра сигнала (например, напряжения или тока) от времени (рисунок 9). На временной диаграмме сигнала можно наблюдать форму сигнала. Временную диаграмму (осциллограмму) можно визуально наблюдать с помощью специального измерительного прибора — осциллографа.
Рисунок 9 - Временные диаграммы сигналов
Векторная диаграмма используется при изучении процессов связанных с изменением фазы сигнала (например, при фазовой модуляции). В данной диаграмме сигнал представляется вектором, длина которого пропорциональна амплитуде сигнала, а угол наклона относительно исходного вектора показывает фазу сигнала (рисунок 10).
Рисунок 10 - Векторная диаграмма сигнала
В геометрической диаграмме сигнал представляется в виде геометрического фигуры. Данная диаграмма может быть использована при визуальном представлении объема сигнала.
Спектральная диаграмма представляет собой график распределения энергии (спектр амплитуд) или фаз (спектр фаз) сигнала по частотам. Более подробно данный способ представления сигналов будет описан ниже. Данные диаграммы можно наблюдать с помощью специального измерительного прибора — анализатора спектра.
Математические модели сигналов
Математической моделью сигнала называется математическое выражение, по которому можно определить значения сигнала в любой момент времени.
Математические модели необходимы для изучения сигналов и моделировании электрических цепей.
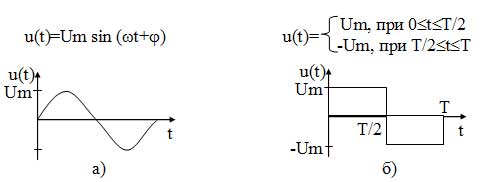
Математическая модель может быть задана формулой (рисунок 11а) либо математическим условием (рисунок 11 б)
Рисунок 11 - Способы задания математических моделей
Приведенные выше сигналы являются простыми по форме. Сложные сигналы описать подобными выражениями нельзя. Математическую модель таких сигналов можно записать в виде ряда:
где ak — коэффициенты пропорциональности;
?k (t) — элементарные базисные функции.
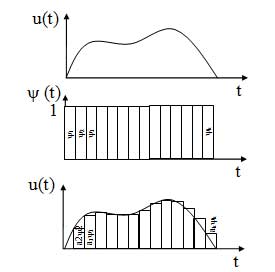
т. е. сложный сигнал можно представить в виде суммы элементарных (простейших) базисных функций (сигналов) амплитуда которых будет зависеть от значений описываемого сигнала. Например, нужно описать сигнал u(t) представленный на рисунке 12. Возьмем в качестве базисных функций прямоугольные импульсы, сдвинутые один относительно другого на длительность импульса ? и имеющие единичную амплитуду. Затем амплитуды этих импульсов уменьшим до мгновенных значений описываемого сигнала в каждый конкретный момент времени. Значение амплитуды в этом случае будет являться коэффициентом пропорциональности (ak). Таким образом, сигнал будет представлен множеством импульсов с различными амплитудами и сигнал может быть представлен записанным выше рядом. Точность описания сигнала определяется количеством слагаемых ряда и формой базисных функций: чем больше нужна точность сигнала, тем больше слагаемых должен иметь ряд (необходимо уменьшать длительность импульсов). В качестве базисных функций могут быть
Рисунок 12 - Представление сложного сигнала базисными функциями
использованы любые функции, но при этом они должны быть обязательно простыми. Наиболее удобными в описании и техническом получении являются гармонические функции. При их использовании любой сигнал может быть описан рядом Фурье.