Поскольку все информационные сигналы и помехи являются случайными и могут быть предсказаны лишь с некоторой степенью вероятности, то для описания таких сигналов используется теория вероятностей. При этом используются статистические характеристики, которые получают путем проведения многочисленных опытов в одинаковых условиях.
Все случайные явления, изучаемые теорией вероятностей можно разделить на три группы:
— случайные события;
— случайные величины;
— случайные процессы.
Случайное событие — это всякий факт, который в результате опыта может произойти или не произойти.
Случайным событием является появление помехи на входе приемника или прием сообщения с ошибкой.
Случайные события обозначаются латинскими буквами А, В, С.
Числовыми характеристиками случайного события являются:
1. Частота появления случайного события:
?= m/N (40)
где m — количество опытов, в которых произошло данное событие;
N — общее количество проведенных опытов.
Как следует из выражения (40) частота появления случайного события не может превышать 1, т. к. количество опытов, в которых произошло данное событие не может привысить общее количество проведенных опытов.
2. Вероятность появления случайного события:
Т. е. вероятность появления случайного события есть частота его появления при неограниченном увеличении количества проведенных опытов. Вероятность появления события не может превышать 1. Случайное событие, имеющее вероятность равную единице является достоверным, т. е. оно обязательно произойдет, поэтому такую вероятность имеют уже произошедшие события.
Случайная величина — это величина, которая от опыта к опыту изменяется случайным образом.
Случайной величиной является амплитуда помехи на входе приемника или количество ошибок в принятом сообщении. Случайные величины обозначаются латинскими буквами X, Y, Z, а их значения — x, y, z.
Случайные величины бывают дискретными и непрерывными.
Дискретной называется случайная величина, которая может принимать конечное множество значений (например, количество оборудования, количество телеграмм и т. д., т. к. они могут принимать только целое число 1, 2, 3, …).
Непрерывной называется случайная величина, которая может принимать любые значения из некоторого диапазона (например, амплитуда помехи на входе приемника может принимать любые значения, точно так же как и любые значения может принимать информационный аналоговый сигнал).
Числовыми, статистическими характеристиками, описывающими случайные величины являются:
1. Функция распределения вероятности.
F(x)=P(X ? x) (42)
Данная функция показывает вероятность того, что случайная величина Х не превысит конкретно выбранного значения х. Если случайная величина Х является дискретной, то F(x) так же является дискретной функцией, если Х непрерывная величина, то F(x) ? непрерывная функция.
2. Плотность распределения вероятности.
Р(х)=dF(x)/dx (43)
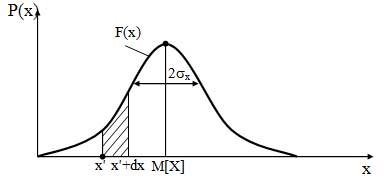
Данная характеристика показывает вероятность попадания значения случайной величины в малый интервал dx в окрестности точки х’, т. е. в заштрихованную область (рисунок).
3. Математическое ожидание.
где хi — значения случайной величины;
Р(хi) — вероятность появления этих значений;
n — количество возможных значений случайной величины.
где р(х) — плотность вероятности непрерывной случайной величины.
По своему смыслу математическое ожидание показывает среднее и наиболее вероятное значение случайной величины, т. е. это значение наиболее часто принимает случайная величина. Выражение (44) применяется, если случайная величина является дискретной, а выражение (45), если она является непрерывной. Обозначение M[X] является специальным для математического ожидания того случайной величины, которая указана в квадратных скобках, однако иногда используются обозначения mх или m.
4. Дисперсия.
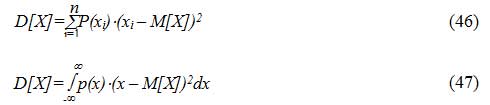Дисперсия количественно характеризует степень разброса результатов отдельных опытов относительно среднего значения. Обозначение дисперсии случайной величины D[X] является общепринятым, однако может использоваться и обозначение ??х. Выражение (46) используется для вычисления дисперсии дискретной случайной величины, а (47) — для вычисления дисперсии непрерывной случайной величины. Если извлечь квадратный корень из дисперсии, то получится величина, называемая среднеквадратическим отклонением (?х).
Все характеристики случайной величины можно показать с помощью рисунка 22.
Рисунок 22 - Характеристики случайной величины
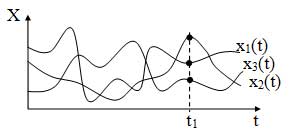
Случайный процесс — это такая функция времени t, значение которой при любом фиксированном значении времени является случайной величиной. Например, на рисунке 23 показана диаграмма некоторого случайного процесса, наблюдаемого в результате проведения трех опытов. Если определить значение функций в фиксированный момент времени t1, то полученные значения окажутся случайными величинами.
Рисунок 23 - Ансамбль реализаций случайного процесса
Таким образом, наблюдение любой случайной величины (Х) во времени, является случайным процессом Х(t). Например, как случайные процессы, рассматриваются информационные сигналы (телефонные, телеграфные, передачи данных, телевизионные) и шумы (узкополосные и широкополосные).
Однократное наблюдение случайного процесса называется реализацией xk(t). Совокупность всех возможных реализаций одного случайного процесса называется ансамблем реализаций. Например, на рисунке 23 представлен ансамбль реализаций случайного процесса, состоящий из трех реализаций.
Для характеристики случайных процессов используются те же характеристики, что и для случайных величин: функция распределения вероятности, плотность распределения вероятности, математическое ожидание и дисперсия. Данные характеристики рассчитываются аналогично, как и для случайных величин. Случайные процессы бывают различных типов. Однако в электросвязи большинство случайных сигналов и помех относятся к стационарным эргодическим случайным процессам.
Стационарным является случайный процесс, у которого характеристики F(x), P(x), M[X] и D[X] не зависят от времени.
Эргодическим является процесс, у которого усреднение по времени одной из реализации приводит к тем же результатам, что и статическое усреднение по всем реализациям. Физически это означает, что все реализации эргодического процесса похожи друг на друга, поэтому измерения и расчеты характеристик такого процесса можно проводить по одной (любой) из реализаций.
Кроме четырех характеристик приведенных выше случайные процессы также описываются функцией корреляции и спектральной плотностью мощности.
Функция корреляции характеризует степень взаимосвязи между значениями случайного процесса в различные моменты времени t и t+?. Где ? временной сдвиг.
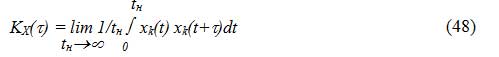где tн — время наблюдения реализации xk(t).
Спектральная плотность мощности — показывает распределение мощности случайного процесса по частотам.
где ?Р — мощность случайного процесса, приходящаяся на полосу частот ?f.
Таким образом, наблюдение случайного явления во времени является случайным процессом, его появление является случайным событием, а его значение случайной величиной.
Например, наблюдение телеграфного сигнала на выходе линии связи в течение, какого то времени — это случайный процесс, появление на приеме его дискретного элемента «1» или «0» — случайное событие, а амплитуда этого элемента — случайная величина.