Цифровые сигналы формируются из аналоговых сигналов в результате трех последовательных процессов:
— дискретизации по времени;
— квантования по уровню;
— кодирования.
Теорема и ряд Котельникова
Дискретизация — процесс преобразования аналогового сигнала в последовательность отсчетов.
Отсчет — мгновенное значение сигнала взятое через определенный интервал времени.
При дискретизации основной задачей является определение временного интервала, через который должны следовать отсчеты сигнала, чтобы при восстановлении этого сигнала не возникало искажений. Поскольку дискретизация используется при организации многоканальной системы передачи с временным разделением каналов (МСП с ВРК), где в интервале между соседними отсчетами одного сигнала передаются отсчеты других сигналов, то существует прямо пропорциональная зависимость между интервалом следования отсчетов и количеством организуемых каналов: чем меньше временной интервал между отсчетами, тем меньше каналов может быть организовано в одной линии связи, и на оборот. Следовательно, чем больше интервал, тем больше каналов можно организовать в одной линии связи, однако при большом временном интервале сигнал будет искажен при восстановлении. Таким образом, необходимо определить такие условия, при которых сигнал будет восстанавливаться без искажений и количество каналов будет максимальным. Данная задача решается теоремой, сформулированной В. А. Котельниковым которая заключается в том, что любой непрерывный сигнал, ограниченный по спектру частотой Fmax (Fв), может быть представлен своими мгновенными значениями, следующими через интервал времени ?t
?t=1/(2fmax) (32)
Интервал ?t называется интервалом или шагом дискретизации, а величина 2fmax называется частотой дискретизации (fд).
Данная теорема основана на том, что реальные непрерывные сигналы являются сравнительно плавными функциями и скачков значений в них практически не наблюдается.
Восстановление сигнала осуществляется с помощью ряда Котельникова:
![]() где: k — номера отсчетов k=1, 2, 3 …
где: k — номера отсчетов k=1, 2, 3 …
?д = 2? 2fmax
Коэффициенты разложения U(k?t) соответствуют отсчетам непрерывного сигнала u(t) в моменты k?t.
В ряде Котельникова выражение
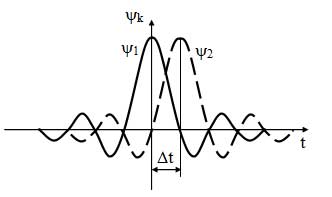
sin ?д(t – k?t)/ ?д(t – k?t)= ?k
является функцией отсчетов. Они имеют одинаковую форму вида sin x/x и отличаются друг от друга временным интервалом ?t. Графики функций остчетов показаны на рисунке 19. Высота функций отсчетов зависит от коэффициентов разложения. Сложение значений функций ?k в любой момент времени дает значение непрерывного сигнала (рисунок 20).
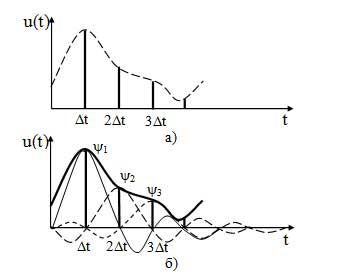
Рисунок 20 - Представление сигнала рядом Котельникова а) сигнал u(t) и его отсчеты; б) сумма ряда Котельникова
Функция отсчета является импульсной реакцией идеального фильтра низких частот при подаче на его вход отсчета U(k?t) в момент времени k?t. Таким образом, восстановление сигнала, представленного своими отсчетами, осуществляется ФНЧ. Однако, при использовании реальных фильтров частоту дискретизации принимают равной на 15 – 20% выше теоретически рассчитанной.
Квантование
Квантование — процесс округления дискретных отсчетов по амплитуде то определенных уровней, называемых разрешенными или уровнями квантования.
Расстояние между соседними уровнями называется шагом квантования ?u.
Если при квантовании амплитуда отсчета попадает между соседними уровнями, то она округляется до ближайшего по правилу: если амплитуда меньше половины шага квантования (?u/2), то она округляется к меньшему уровню квантования, если амплитуда равна или больше ?u/2, то округляется к большему уровню.
Поскольку квантование связано с изменением амплитуд отсчетов сигнала, то при квантовании возникают искажения называемые ошибкой квантования или шумом квантования (?кв). Ошибка квантования не превышает половины шага квантования
?кв ? ?u/2. (34)
Ошибка квантования для k-го отсчета определяется как
?квk=Uквk(k?t) — Uk(k?t) (35)
где Uквk(k?t) — амплитуда k-го отсчета после квантования;
Uk(k?t) — амплитуда k-го отсчета до квантования.
Как следует из выражения (35) ошибка квантования может быть как положительной, так и отрицательной, причем если она положительна, то происходит увеличение амплитуды отсчета при квантовании, если отрицательна, то происходит уменьшение амплитуды отсчета.
Ошибка квантования, согласно (34) определяется шагом квантования и не зависит от посторонних воздействий на сигнал (помех). В свою очередь шаг квантования зависит от количества уровней квантования и амплитуды сигнала и определяется как
?u = Um(t)/(Lкв — 1) (36)
где Um(t) — амплитуда аналогового сигнала, подвергаемого дискретизации и квантованию (либо наибольшая амплитуда последовательности отсчетов):
Lкв — количество уровней квантования.
Выражение (36) справедливо для униполярных (однополярных сигналов), если же используются биполярные сигналы, то;
?u = 2Um(t)/(Lкв — 1) (37)
Из выражений (36) и (37) следует что для уменьшения шага квантования необходимо увеличивать количество уровней квантование, однако слишком большое количество уровней квантования также не целесообразно, т. к. приводит к увеличению разрядности кодовых комбинаций цифрового сигнала, увеличению вероятности ошибки и как следствие, уменьшению помехоустойчивости.
Квантование может быть равномерным и неравномерным. При равномерном квантовании шаг квантования остается постоянным для всех уровней, а при неравномерном квантовании шаг квантования изменяется. Применение неравномерного квантования позволяет уменьшить шум квантования.
Кодирование
Процесс кодирования при формировании цифровых сигналов заключается в замене значения амплитуды каждого дискретного квантованного отсчета кодовой комбинацией двоичного кода. Причем кодируется не абсолютное значение амплитуды, а номер уровня квантования, которому соответствует данная амплитуда. Важной характеристикой кодера при этом является разрядность кодовой комбинации (n), под которой понимают количество элементов используемых в одной кодовой комбинации. Разрядность кодовой комбинации зависит от количества уровней квантования и определяется для равномерного двоичного кода как
n = log2Lкв. (38)
При заданной разрядности Lкв определяется из выражением
Lкв = 2n (39)
Таким образом, важными характеристиками при преобразовании аналогового сигнала в цифровой являются:
— шаг дискретизации;
— шаг квантования;
— разрядность кодовой комбинации.
Процесс формирования цифрового сигнала представлен на рисунке 21.
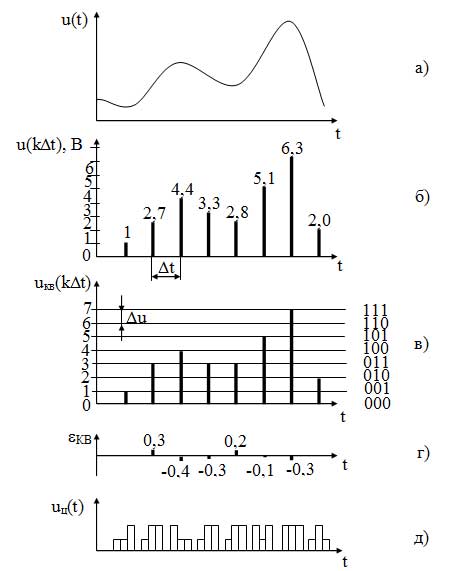
Рисунок 21 - Формирование цифрового сигнала: а) аналоговый сигнал; б) дискретнзация; в) квантованный сигнал; г) ошибка квантования; д) цифровой сигнал.