Эффективное кодирование

Как известно, большинство сообщений, формируемых источником, содержат избыточность. Удаление или уменьшение избыточности является одной из задач кодирования.

Кодирование, которое осуществляет удаление или уменьшение избыточности из закодированных сообщений, называется эффективным.

Возможность эффективного кодирования основана на теореме Шеннона, согласно которой:

Минимальное среднее количество элементов на выходе кодирующего устройства, соответствующее одному символу дискретного сообщения, можно сделать сколь угодно близким к максимальной энтропии источника.

Эффективное кодирование осуществляется с применением неравномерных кодов, в которых более короткие кодовые комбинации соответствуют более вероятным символам сообщения, а более длинные — менее вероятным символам.

Основными требованиями, предъявляемыми к эффективному коду, являются:

• однозначность декодирования, т. е. каждому символу кодируемого сообщения должна соответствовать своя кодовая комбинация и для всех символов комбинации должны быть различны;
• в среднем на один символ сообщения должно приходиться минимальное число элементов кодовой комбинации эффективного кода;
• ни какая более короткая комбинация эффективного кода не должна являться началом другой, более длинной комбинации.

Рассмотрим построение эффективного кода на примере кода Шеннона-Фано и кода Хаффмена.

Пример 1. Источник вырабатывает восемь сообщений с вероятностями Р(а₁) = Р(а₄) =0,25; Р(а₅) = Р(а₇) = 0,125; Р(а₂) = Р(а₃) = Р(а₆) = Р(а₈) = 0,0625. Осуществить эффективное кодирование кодом Шеннона-Фано.

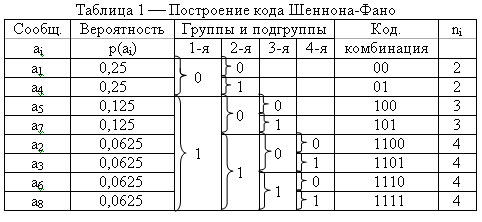
Для построения кода необходимо составить таблицу 1.

Заполнение таблицы осуществляется в три этапа.

1 этап. Записываются сообщения a_i в порядке убывания их вероятностей (более вероятные вверху, менее вероятные внизу).

2 этап. Все сообщения делятся на две группы, таким образом, чтобы в каждой группе суммарные вероятности были примерно равны. Верхней группе присваивается ноль нижней единица. Затем каждая группа разбивается на две подгруппы, также, по возможности,  с равными суммарными вероятностями. Верхней подгруппе присваивается ноль, нижней единица, и т. д. Деление подгрупп производится до тех пор, пока в каждой подгруппе не окажется по одному элементу a_i.

3 этап. Записываются кодовые комбинации, соответствующие каждому элементу сообщения, при этом 1-я группа соответствует старшему разряду, 2-я следующему и т. д. по всем столбцам. Если в столбце элемента a_i отсутствует символ «0» или «1», то в соответствующем разряде кодовой комбинации он не пишется.

Как видно из таблицы, каждому элементу a_i соответствует своя, нигде не повторяющаяся, кодовая комбинация. Ни одна более короткая кодовая комбинация не является началом другой более длинной. При этом более вероятные символы сообщения имеют более короткие комбинации, а менее вероятные — более длинные.

Определим, удалена ли избыточность в результате кодирования.

Энтропия, приходящаяся на один символ сообщения, определяется как

Максимальная энтропия источника формирующего восемь сообщений равна

Нmax(A) = log₂N_a = log₂ 1/8 = 3 бит/сообщ.

Избыточность сообщения вырабатываемого источником равна

c_с = (Нmax(A) – Н(А))/Нmax(А) = (3 – 2,75)/3 = 0,09

Для определения избыточности сообщения после кодирования определим среднюю длину кодовой комбинации

Энтропия, приходящаяся на один разряд кодовой комбинации, определяется как

Нр(А) = Н(А)/n_ср = 2,75/2,75 = 1 бит/разряд

Максимальная энтропия на выходе двоичного дискретного источника равна

Нmax(А) = log₂2 = 1 бит/сообщ.

Определим коэффициент избыточности источника.

c_с = (1 – 1)/1 = 0

Таким образом, избыточность удалена.

Пример 2. По приведенным в примере 1 данным необходимо осуществить эффективное кодирование кодом Хаффмена.

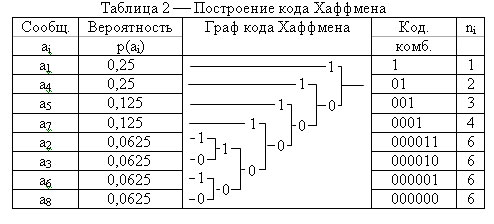
Построение данного кода, также удобно оформить в виде    таблицы 2.

Таблица заполняется следующим образом.

1 этап. Записываются сообщения a_i в порядке убывания их вероятностей (более вероятные вверху, менее вероятные внизу).

2 этап. Строится дерево кода, для этого два сообщения с наименьшей вероятностью (снизу таблицы) объединяются в группу. Верхней ветви присваивается единица, нижней ? ноль. Если четыре символа имеют одинаковую минимальную вероятность, то организуются две одинаковые группы. Затем формируется следующая группа: нижняя ветвь графа исходит из предыдущей группы, а верхняя ? из следующего элемента, расположенного на одну позицию выше (этот элемент может иметь большую вероятность, или такую же, как и в предыдущей группе). Верхней ветви присваивается единица, нижней ? ноль. Такая организация групп продолжается до тех пор, пока не образуется последняя группа с элементом имеющим наибольшую вероятность ( в самом верху таблицы).

3 этап. Формируются кодовые комбинации, для этого записывают значение ветвей графа справа налево.

n_ср = 3,125